The Cubic Crystal System

The cubic crystal system is defined as having the symmetry of a cube: the conventional unit cell can be rotated by 90$^\circ$ about any axis, or by 180$^\circ$ around an axis running through the center of two opposing cube edges, or by 120$^\circ$ around a body diagonal, and retain the same shape. The conventional cell then takes the form
\[ \begin{array}{ccc} \mathbf{A}_1 & = & a \, \mathbf{\hat{x}} \nonumber \\ \mathbf{A}_2 & = & a \, \mathbf{\hat{y}} \nonumber \\ \mathbf{A}_3 & = & a \, \mathbf{\hat{z}}, \end{array} \] with unit cell volume \[ V = a^3\].
This is the limiting case of both the orthorhombic and tetragonal systems when all primitive vectors are equal in length.
There are three Bravais lattices in the cubic system.
Lattice 12: Simple Cubic
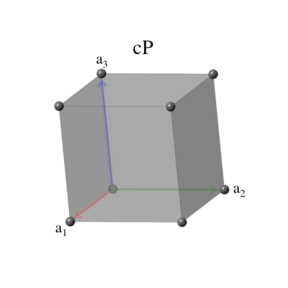
The simple cubic system is identical to the conventional cubic unit cell:
\[ \begin{array}{ccc} \mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \nonumber \\ \mathbf{a}_2 & = & a \, \mathbf{\hat{y}} \nonumber \\ \mathbf{a}_3 & = & a \, \mathbf{\hat{z}}, \end{array} \] with volume \[ V = a^3. \]
This can also be considered as a rhombohedral lattice with $\alpha = \pi/2$. The space groups associated with this lattice are
\[ \begin{array}{lll} 195. ~ \text{P23} & 198. ~ \text{P2$_{1}$3} & 200. ~ \text{Pm$\overline{3}$} \\ 201. ~ \text{Pn$\overline{3}$} & 205. ~ \text{Pa$\overline{3}$} & 207. ~ \text{P432} \\ 208. ~ \text{P4$_{2}$32} & 212. ~ \text{P4$_{3}$32} & 213. ~ \text{P4$_{1}$32} \\ 215. ~ \text{P$\overline{4}$3m} & 218. ~ \text{P$\overline{4}$3n} & 221. ~ \text{Pm$\overline{3}$m} \\ 222. ~ \text{Pn$\overline{3}$n} & 223. ~ \text{Pm$\overline{3}$n} & 224. ~ \text{Pn$\overline{3}$m} \\ \end{array} \]
Lattice 13: Face-Centered Cubic
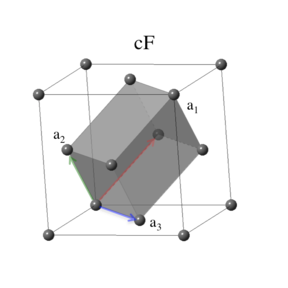
The face-centered cubic lattice has the same periodicity as its simple cubic parent with the addition of a translation from one corner of the cube to the center of any face. Our standard face-centered cubic primitive vectors have the form
\[ \begin{array}{ccc} \mathbf{a}_1 & = & \frac{a}{2} \, \mathbf{\hat{y}} + \frac{a}{2} \, \mathbf{\hat{z}} \\ \mathbf{a}_2 & = & \frac{a}{2} \, \mathbf{\hat{x}} + \frac{a}{2} \, \mathbf{\hat{z}} \\ \mathbf{a}_3 & = & \frac{a}{2} \, \mathbf{\hat{x}} + \frac{a}{2} \, \mathbf{\hat{y}}, \end{array} \]
and the primitive cell volume is
\[ V = \frac{a^3}{4}. \]
There are four face-centered cubic primitive cells in the conventional cubic cell. The face-centered cubic lattice can also be considered as a rhombohedral lattice where $\alpha = 60^\circ$. The space groups associated with this lattice are:
\[ \begin{array}{lll} 196. ~ \text{F23} & 202. ~ \text{Fm$\overline{3}$} & 203. ~ \text{Fd$\overline{3}$} \\ 209. ~ \text{F432} & 210. ~ \text{F4$_{1}$32} & 216. ~ \text{F$\overline{4}$3m} \\ 219. ~ \text{F4$\overline{3}$c} & 225. ~ \text{Fm$\overline{3}$m} & 226. ~ \text{Fm$\overline{3}$c} \\ 227. ~ \text{Fd$\overline{3}$m} & 228. ~ \text{Fd$\overline{3}$c} & \\ \end{array} \]
Lattice 14: Body-Centered Cubic

Like its predecessors in the orthorhombic and tetragonal systems, the body-centered cubic crystal has the same periodicity as its parent with the addition of a translation from one corner of the cube to its center. Our standard body-centered cubic primitive vectors have the form:
\[ \begin{array}{ccc} \mathbf{a}_1 & = & - \frac{a}{2} \, \mathbf{\hat{x}} + \frac{a}{2} \, \mathbf{\hat{y}} + \frac{a}{2} \, \mathbf{\hat{z}} \\ \mathbf{a}_2 & = & ~ \frac{a}{2} \, \mathbf{\hat{x}} - \frac{a}{2} \, \mathbf{\hat{y}} + \frac{a}{2} \, \mathbf{\hat{z}} \\ \mathbf{a}_3 & = & ~ \frac{a}{2} \, \mathbf{\hat{x}} + \frac{a}{2} \, \mathbf{\hat{y}} - \frac{a}{2} \, \mathbf{\hat{z}}, \end{array} \] and the primitive cell volume is \[ V = \frac{a^3}{2}. \]
There are two body-centered cubic primitive cells in the conventional cubic cell. The body-centered cubic lattice can also be considered as a rhombohedral lattice where $\alpha = \cos^{-1}(-1/3) \approx 109.47^\circ$. The space groups associated with this lattice are:
\[ \begin{array}{lll} 197. ~ \text{I23} & 199. ~ \text{I2$_{1}$3} & 204. ~ \text{Im$\overline{3}$} \\ 206. ~ \text{Ia$\overline{3}$} & 211. ~ \text{I432} & 214. ~ \text{I4$_{1}$32} \\ 217. ~ \text{I$\overline{4}$3m} & 220. ~ \text{I$\overline{4}$3d} & 229. ~ \text{Im$\overline{3}$m} \\ 230. ~ \text{Ia$\overline{3}$d} & ~ & ~ \\ \end{array} \]